Measuring Color

• The Color Wheel

  

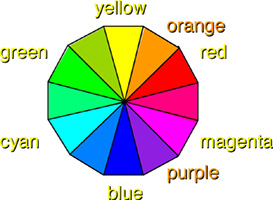
  In both the additive and subtractive color systems, each color has a set place among the others. For example, while red and blue add to make magenta, that same magenta can combine subtractively with cyan to make blue again, and that same blue can add to green to produce the same cyan. This procession of colors eventually overlap; once all colors are used up the sequence repeats. This may be represented as a color wheel where every color is created by combining the two colors to either side of it. If this process is continued until each single block of color is indeterminately small, a continuous color wheel will have been produced. All colors in the wheel may be created either additively or subtractively from the corresponding primaries.

  It is important to note that even this color wheel is limited in the colors it contains. The most intense red, for example, is the primary or secondary red color with which we started. If there exists a more pure red than the one we used, we will not be able to create it through combining our red with other colors and thus it will not appear anywhere on our color wheel.

  This limitation preventing the production of colors more pure than the particular primaries is inherent in all color systems. The range of colors which a given set of primaries within a color system can produce is referred to as its color gamut. As we shall see, color gamuts can vary tremendously depending upon the three colors chosen as primaries. Real-world color gamuts are further limited by the imperfections in the primaries and in their combinational implementation. This is the fiction of color.

  Color Specification

  One way to define a colorant might be by its energy spectrum; this definition, however, creates two problems. The first is that we would have to specify the energy level at a relatively large number of wavelengths (perhaps 32 or more). More importantly, there is no direct link between color perception and this method of specification or between colors that were perceived to be similar through the human visual system (e.g., our banana spectral response vs. pure yellow).

  Perhaps the most intuitive way to look at color is by expanding the color wheel. Circularly traversing the wheel, color varies by angle. However, no matter how we affect this angle, we cannot describe white, black, or any transition from a pure color to white or black. So rather than call this angular component the color, we refer to it merely as hue, that component of a color definition which determines the proportions of the color determining primaries.

  Using our primaries to produce black or white is trivial, at least theoretically: we mix all three additive colors for white, remove them for black, etc. While combining two primaries produces another saturated color, combining all three in equal proportions produces a neutral gray, white, or black, depending on the amount. We can put these neutrals in the center of the color wheel, and allow a smooth transition from this unsaturated neutral to the fully saturated color wheel. The distance from the center is the saturation or chroma.

  We can now produce any hue by varying the proportions of the two strongest primary colors; we can affect the saturation by adjusting the amount of the weaker primaries to, in effect, add black or white to a color. If we remove all saturation from a color—change it completely to neutral gray—we still have the problem of representing the difference between white and black. We can create a vertical axis called lightness (also referred to as brightness, or value), perpendicular to the color wheel, which runs from black through gray to white (although mid-gray may not be at the same place on each scale). These three axes create a three-dimensional coordinate system based on the color wheel.

  It is not a coincidence that this number of parameters matches the human visual system’s three sensors. In general, a color system requires three independent variables. From this comes the notion of a color space. Like the three dimensions of physical space, color definition requires three independent parameters. The ability of a spatial color plot both to describe colors accurately and to provide an intuitive way to think of color makes a three-dimensional space based on the color wheel quite desirable. If saturation is the distance from the lightness axis and fully saturated colors have no white or black component, changing the lightness of a fully saturated color will always decrease its saturation. This relationship between saturation and lightness is most evident when looking at pure white or black: color is completely absent from both—they have no saturation at all; thus, any attempt to increase saturation must decrease the amount of black or white from 100% to some lesser value. Since the overall gray level is thus changed, a change in the color’s brightness has been forced in order to affect its saturation. In this manner, this color system has a physical limitation: it tapers as it gets closer to 100% white or black, so, in effect, our initial color wheel has been transformed into a spherical color space.

  CIE Color

  As we have seen, color can be artificially created. Light sources work as an additive color system, and objects work as a subtractive color system. However, we still have no method of defining a specific color. From our discussion of color gamut, it should be clear that there exists some range of colors which we would casually call red. Roses are red, and fire engines are (or used to be) red, but they’re not the same red. What then is red? To answer this question we must create a definition of the color we perceive so that we can reproduce it and agree that it is the same color. Furthermore, we want to have some specification of the color, so that we can easily communicate our definition of it and measure the difference between any two colors.

  

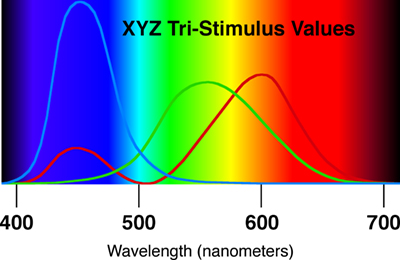
  In 1931 the CIE initially attempted to standardize color perception. This committee found that while colorants could be classified technically by their energy absorption spectra, these specifications did not adequately define color. However, color as a visual effect could be specified by the amounts of light received by the three receptor cones in the human eye. The CIE established a standard observer to provide a baseline by which to define color. Additionally, the CIE established standards for illuminants. With a carefully defined illuminant and observer, object colorants could be characterized. Specific wavelengths for color primaries were chosen, and the intensity of each necessary to create the spectral colors were ascertained. These resulting CIE color matching functions were transformed to eliminate negative portions and to make the mid-bandwidth function identical to the brightness response of the visual system. Called the X, Y, and Z Tri-stimulus values, they correspond roughly to red, green, and blue.

  These values were useful in that mathematical conversions could be found that would transform them into corresponding values for different color primaries or color systems. This property introduced the idea of an independent color space—standardized color parameters that could be transformed mathematically to any color model. While XYZ values were mathematically useful to describe color, more intuitive methods were sought which did not lose the functionality of independent color.

  As a side note, the CIE color space does not deal with all colors, such as fluorescent or metallic colors, due to their more complex spectral transfer functions. For example, if we measured the spectral response of pink fluorescent paper, more than 100% of the incident light energy is reflected in the red range. This is due to a conversion of light energy from the ultraviolet to the red wavelengths, a complex energy transformation which lies outside the realm of CIE color spaces.

  

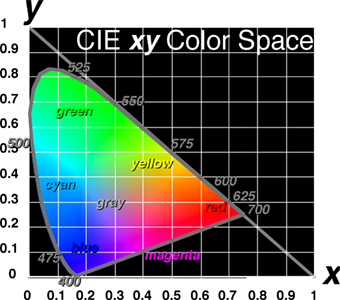
  The simplest change made to the XYZ space was a normalization of intensity. Since the total intensity of a color is the sum X+Y+Z, dividing by this sum normalizes the intensities and results in the parameters called x, y, and z. This is useful in two ways: only two values, such as x and y, need be provided (the third can be derived from the fact that x+y+z=1). Secondly, color can be specified other than intensity, and therefore plotted in only two dimensions. To recover the intensity value, colors are described by x, y, and Y values so that the X and Z components can be reconstituted based on the ratio of y to Y. This specification is referred to as the CIE xyY color space.

  One significant problem with the xyY space is that it is a far reach from the friendly color wheel. In 1947, Hunter formalized the Lab color space, wherein yellow is given more of its rightful due than in the color wheel. L represents lightness, a is the red-greenness, and b is the yellow-blueness (notice the similarity to the Opponent-Process Theory).

  In 1976, the CIE adapted Hunter’s space into the L*a*b* space. It developed an explicit mathematical relation for the conversion of colors from XYZ space into L*a*b* space, retaining the general characteristics of Hunter’s Lab. By defining a standard unit of color difference, the ΔE, Hunter made a major improvement on the issue of color matching and error measurement. Hunter mapped the color space so that equal distances in the graphical model approximated equal changes in color (not at all true for xyY space). Hunter defined ΔE = √(ΔL² + Δa² + Δb²) and proposed that a single ΔE represents the minimum human-discernible color difference: anything less is undetectable by the average human eye. Although the L*a*b* space is not ideally uniform, so the ΔE is not a very precise source of difference information, a ΔE of 10 will always be noticeable, and a ΔE of 0.1 will be indistinguishable to almost all observers. Like a color wheel defined on cylindrical coordinates, this same idea can be used in the L*a*b* space. The lightness axis is still represented by L*. Saturation or Chroma is √(Δa²+Δb²), the length of the radius to the a* and b* values, and the Hue is arctan(b*÷a*). This rectangular to cylindrical conversion transforms the CIE L*a*b* into the LCH (Lightness, Chroma, and Hue) color space.