Color Theory

• Opponent-Process Theory

  To probe deeper for a moment, according to the Opponent-Process theory, the eye combines long wavelength (red) and medium wavelength (green) responses and compares the combination (yellow) to the short wavelength (blue) response—to create a yellow-blue difference. Similarly, the eye combines short wavelength (blue) and long wavelength (red) responses and compares that combination (magenta) to the medium wavelength (green) response—to create the green-magenta difference. The presence or absence of all three responses creates the white-black difference. These three differences—yellow-blue, green-magenta, and white-black—are then combined by the brain into the perception of a single color. For example, blue (without yellow) and green (without magenta) with a neutral whiteblack would yield a strong cyan.

  Although the Opponent-Process theory provides a reasonably good explanation of color vision phenomena, it remains a theory with room for further understanding. Two earlier theories are worth noting, the Component Theory and the Opponent Theory.

  The Component theory, initially proposed in the nineteenth century by Thomas Young and later refined by H.L.F. von Helmholtz, holds that the simple combination of two cone responses yields a particular color sensation; for example, the combination of blue and green cone responses would cause a cyan sensation. We have learned that three cone responses are not uniquely red, green, and blue, and that they tend to be much broader than suggested by this theory.

  The Opponent theory, developed by Ewald Hering in the 1870s, introduced the concept of red-green and blue-green opponent sensitivity as well as whiteblack relative contrast. However, it assumes the existence of a red-green receptor capable of separate responses and fails to explain the different red-green blindnesses currently known.

  The Opponent-Process theory adds refinements to better explain afterimage, simultaneous color contrast, edge contrast, and other issues beyond the current scope.

  Additive Color Theory

  

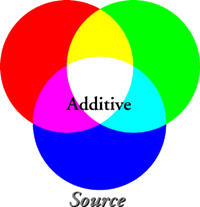
  At any single time and place, the brain combines the three cone stimuli into a single color perception. This suggests an interesting possibility: if we send just three color values to a point on the retina, the brain will translate these values into the single corresponding color. In fact, a full image made up only of red, green, and blue light sources could appear to range the entire color spectrum.

  Because adding these three stimuli can create the experience of full color, they are referred to as color additive primaries. If all three colors are combined in equal strengths, the perception of white is created. If only two are combined in equal strengths, the additive secondaries of cyan (green + blue), magenta (red + blue), and yellow (red + green) are created. So if we can specify merely the presence or absence of a primary, we can create eight distinct colors: three primaries, three secondaries, white (red + green + blue), and black (the lack of all three).

  By continuously varying the intensity of each primary, this color system could create nearly the same perception as the full color spectrum. Because colors are created by adding varying intensities of light, this is referred to as an additive color system.

  Since the illuminant and colorant are one and the same for additive color systems, the effects of changing the illuminant are easily controlled. CRTs—color television and computer monitors—are a common and significant example of additive color.

  Subtractive Color Theory

  

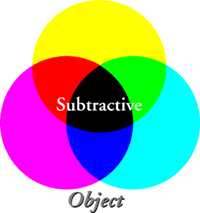
  What happens if a transparent object transmits some wavelengths more than others? For example, consider an object that only transmits wavelengths near 575 nm (yellow). It would act as a filter, absorbing (or reflecting) blue-green and red. The filter might be made up of two filters, one passing the band of frequencies above 575 nm (yellow and red) and one passing the band below 575 nm (yellow, green and blue). The first filter removes (subtracts) green and blue, while the second removes (subtracts) red; together they remove (subtract) both blue-green and red, as above.

  Unlike the additive color in the simple illuminant-observer system, transparent filters operate as a subtractive color system. Starting with a broadband white illuminant, a filter that subtracts blue leaves green and red portions of the visible spectrum which are perceived as yellow. A filter that subtracts red leaves green and blue, or cyan. And a filter that subtracts green leaves red and blue, or magenta.

  What happens if a reflective object reflects some wavelengths more than others? If we attached the subtractive filters from above onto a uniformly reflective white surface, we would have such a situation. If we made these filters dispersive, such that on the average the light only went halfway through before reflecting back, the object we made would behave the same as the transmissive one. Such filters, usually called colorants, inherently exist in any object. Both transmissive and reflective objects filter out light energy, operating as subtractive color systems.

  Since we cannot source light energy from a sheet of paper, it must be generated by some active source, thus making additive color impractical for hardcopy reproduction. Even the colors in slide photography, which require a light source to shine through the image, do not follow the additive model; an increase in the slide’s color density represents a decrease in the amount of light transmitted and observed. Printing systems produce color by varying amounts of pigments which absorb light energy, and are subtractive color systems. Such pigments, either in the form of printed inks or filters, can be placed permanently on a surface, causing it to retain the desired color effect.

  In subtractive systems, as in additive ones, the objective is to vary the amount of light that will ultimately enter the human eye. Since the eye responds to the red, green, and blue additive primaries, the primaries used in subtractive systems must allow the ability to add or remove a single color. In conventional printing we use pigments or inks that absorb blue (leaving yellow), green (leaving magenta), and red (leaving cyan). Each subtractive primary absorbs a single color: yellow, the mix of red and green, absorbs blue; magenta, the mix of red and blue, absorbs only green; and cyan, the effect of mixing green and blue light, absorbs only red. While each of these primaries allows two colors to remain in the image, it subtracts a single color, allowing control over the amount of that single color delivered to the eye.

  Just as the additive system has secondary colors, so does the subtractive. Since subtractive primaries each remove a single color of light, combining any two will leave only one of the three remaining. Thus, the subtractive secondaries are the three additive primaries themselves, namely red, green and blue.

  Bananas

  The spectral reflectance of a ripe banana is a simple but interesting measurement. Somewhat surprisingly, the banana reflects green and red, as well as yellow. In other words, it absorbs (or subtracts) blue. Since an observer will perceive the combination of green and red as yellow, the overall effect is a bright yellow.

  Consider for a moment what would happen to perception if we replaced the “uniform broadband illuminant” used in a spectrodensitometer with ideal red light, spectral energy only in the 600-700 nm band. Our banana would look light gray—but an object having an alternate “yellow” spectral distribution in the 550-600 nm band would look almost black.

  If we shine only pure blue light on the fire truck, we see black because the same colorant that previously appeared yellow (or red) continues to absorb the blue region of the light. In this situation, however, no additional light exists and we the resultant absence of light we call black. So, the fire engine is not yellow (or red); it merely looks that color under most ordinary lighting to most ordinary humans.

  It should be clear in the illuminant-object-observer relationship that changing the independent illuminant is just as important as changing the object. Changes to this illuminant can significantly alter the color perception of an object. Thus, while the perceived color from a subtractive reproduction may match a specific colorant under one light condition, it may appear very different under another.